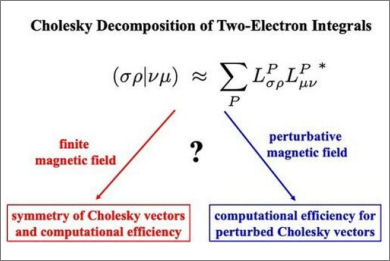
A rigorous analysis is carried out concerning the use of Cholesky decomposition (CD) of two-electron integrals in the case of quantum-chemical calculations with finite or perturbative magnetic fields and gauge-including atomic orbitals. We investigate in particular how permutational symmetry can be accounted for in such calculations and how this symmetry can be exploited to reduce the computational requirements. A modified CD procedure is suggested for the finite-field case that roughly halves the memory demands for the storage of the Cholesky vectors. The resulting symmetry of the Cholesky vectors also enables savings in the computational costs. For the derivative two-electron integrals in case of a perturbative magnetic field we derive CD expressions by means of a first-order Taylor expansion of the corresponding finite magnetic-field formulas with the field-free case as reference point. The perturbed Cholesky vectors are shown to be antisymmetric (as already proposed by Burger et al. [ J. Chem. Phys. 155, 074105 (2021)]) and the corresponding expressions enable significant savings in the required integral evaluations (by a factor of about four) as well as in the actual construction of the Cholesky vectors (by means of a two-step procedure similar to the one presented by Folkestad et al. [J. Chem. Phys. 150, 194112 (2019)] and Zhang et al. [J. Phys. Chem. A 125, 4258–4265 (2021)]). Numerical examples with cases involving several hundred basis functions verify our suggestions concerning CD in case of finite and perturbative magnetic fields.
Gauss, J.; Blaschke, S.; Burger, S.; Nottoli, T.; Lipparini, F. & Stopkowicz, S.
Mol. Phys., e2101562 (2022) https://doi.org/10.1080/00268976.2022.2101562